How to get nth fibonacci number in JavaScript?

2016-07-19

自问

In mathematics, the Fibonacci numbers are the numbers in the following integer sequence, called the Fibonacci sequence:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …

By definition, the first two numbers in the Fibonacci sequence are either 1 and 1, or 0 and 1, depending on the chosen starting point of the sequence, and each subsequent number is the sum of the previous two.

A simple version

function fibonacci(n) {
  if (n < 0) throw Error('Wrong arguments! Natural numbers only!')
  return n < 2 ? n : fibonacci(n - 1) + fibonacci(n - 2)
}
fibonacci(50)

The simplest version takes many unnecessary caculations during the process. There are many redundancy in the fibonacci(n-1) and fibonacci(n-2).

This kind of recursion is called tree recursion. How about doing the recursion linearly?

Linear Recursion

function fibonacci(n) {
  if (n < 0) throw Error('Wrong arguments! Natural numbers only!')
  else {
    function iter(cur, next, count) {
      if (count === 0) return cur
      return iter(next, cur + next, count--)
    }
    return iter(0, 1, n)
  }
}

By this way, the recursion becames linear with O(n) time complexity. It’s much faster than the tree recursion version. The reason behind it is that it always cache the latest two result which the tree recursion does not.

How about we create a Map that cache the result of n once we caculate it?

Memoization

let fibonacci = (function() {
  let memo = {}
  return function f(n) {
    if (n < 0) throw Error('Wrong arguments! Natural numbers only!')
    else {
      if (n in memo) return memo[n]
      else {
        let cache;
        if (n < 2) cache = n
        else cache = f(n - 1) + f(n - 2)
        memo[n] = cache
        return memo[n]
      }
    }
  }
})()

In this implementation, it caches every caculated fibonacci(n) in memo, which provides better performance than the simplest version. But it takes more spaces than the linear recursion because of the memo.

All of the above implementation will throw RangeError: Maximum call stack size exceeded when n is quite big. So why don’t we try to make use of iteration?

Iteration

function fibonacci (n) {
  if (n < 0) throw Error('Wrong arguments! Natural numbers only!')
  let cur = 0, next = 1
  for (let i = 0; i < n; i++)
    [cur, next] = [next, cur + next]
  return cur
}

By this way, there won’t be RangeError any more!

Benchmark

There is my different implementations: fibonacci.js.

The picture below shows the performance of different implementations.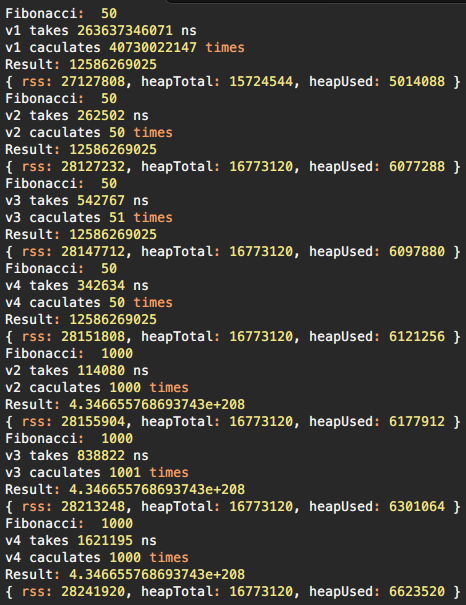
Benchmark

Have Fun

ES6 introduced generators. Try fibonacci with generator: :laughing:

function* fibonacci () {
  let a = 0
  let b = 1
  yield a
  yield b
  while (true) {
    [a, b] = [b, a + b]
    yield b
  }
}
let gen = fibonacci() // Infinite fibonacci number generator!
gen.next().value // Use this to get next fibonacci number

Formula, Lookup Array…

You can read the 3rd reference for more! :yum: